| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Mathematik >
Willkommen/Übersicht > Fotovoltaik >
Fotovoltaik in der Mathematik
Die folgende Unterrichtsskizze beschreibt ein Beispiel der Einbeziehung der Fotovoltaik-Anlage in den Mathematik-Unterricht. Die Stunde wurde -- im Ausbildungsunterricht einer Kollegin -- von einer Referendarin vorbereitet und gehalten. Die Referendarin hat mir dankenswerterweise diese Veröffentlichung gestattet.
Mehr zur Fotovoltaik auf meiner Extra-Seite (s.o., oder am Seitenende)!
zum Seitenanfang / zum Seitenende
Unterrichtsskizze zur Lehrprobe von Elke Hölscher
Klasse:10 a
Ausbildungsschule: Lessing-Gymnasium, Düsseldorf
Fachlehrerin: Frau Friedrichs
Thema der Unterrichtsreihe: Winkelfunktionen
Thema der Unterrichtsstunde: Anwendungen zu Winkelfunktionen in rechtwinkligenDreiecken anhand des Beispiels der optimalen Ausrichtung von Sonnenkollektoren einer Fotovoltaik-Anlage
Lernziele der Stunde
Die Schüler/innen sollen
Stundenverlaufsplan
| Phase | Unterrichtsinhalt | Sozialform | Medium |
| Einstieg | Zwei Schülerinnen halten ein Kurzreferat zum Thema „Fotovoltaik am Lessing-Gymnasium". | SV | Tafel |
| Erarbeitung I | Themenfindung: Die Sch. formulieren nach Betrachtung und Beschreibung der Fotovoltaik-Anlage das Thema der Stunde: ,,Die optimale Ausrichtung von Solarplatten". | UG | Tafel |
| Problemstellung |
Wie muss eine Solarplatte ausgerichtet sein, damit sie die
meisten Sonnenstrahlen auffängt? (*)
Die Sch. erarbeiten eine anschauliche und eine rechnerische Begründung für den optimalen Einfallswinkel von 90 Grad und notieren das Ergebnis auf einem AB. |
UG
EA |
Folien (*)
AB |
| Erarbeitung II |
Die Sch. stellen in Gruppen erste Überlegungen darüber an,
mit welchem Mindestabstand zwei Solarplatten (1 m x 1 m) hintereinander aufgestellt werden sollten, wenn die
Sonne unter 60 Grad Höhenwinkel einstrahlt.
(Zusatz für Schnelle: Wie viele Platten passen dann maximal hintereinander auf ein 12 m langes Flachdach?) |
GA |
AB,
Heft |
| Auswertung | Die Ergebnisse / Zwischenergebnisse (Skizze) werden auf einer Folie präsentiert. | SV | Folie |
| Hausaufgabe | Warum wurden die neun Solarplatten gerade an dieser Stelle und in dieser Formation aufgestellt? (Fakultativ berechnen die Sch. den Mindestabstand zu Hause.) |

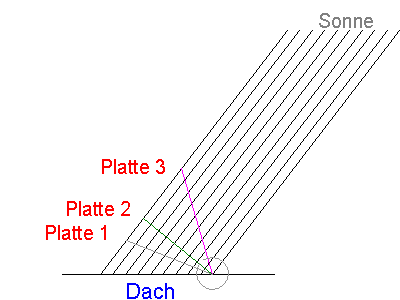
(*) Folie zur Problemstellung:
Bei welchem Winkel fängt eine Solarplatte am meisten Licht ein?
Antwort: Um die gleiche Menge Sonnenlicht einfangen zu können, wie die Solarplatte mit einem Einfallswinkel von 90 Grad (Platte 2 im Bild), müsste eine Platte mit anderem Einfallswinkel länger sein (Platten 1 und 3)!
Mathematische Begründung der Antwort: Bei einem rechtwinkligen Dreieck -- hier z.B. gebildet von der Platte 1 (bzw. 3), der Platte 2 und dem äußersten linken Lichtstrahl -- ist die Hypotenuse länger als die Katheten.
Reflexion der Stunde durch die Referendarin
Die Stunde verlief wie von mir geplant. Das Kurzreferat der beiden Schülerinnen, das von diesen gut vorbereitet und frei vorgetragen wurde, weckte das Interesse der Mitschüler/innen. Durch den Blick aus dem Fenster auf das Dach der Turnhalle konnten sich die Schüler/innen direkt einen guten Überblick über den Aufbau der Fotovoltaik-Anlage verschaffen, so dass ihnen die Formulierung des Stundenthemas keine Schwierigkeiten bereitete.
Die Frage nach dem besten Einfallswinkel der Sonne auf die Solarplatten wurde von einem Schüler formuliert, so dass hieran anknüpfend eine anschauliche und eine mathematische Begründung für den optimalen Einfallswinkel von 90 Grad auf OH-Folien mit Hilfe des Overlay-Verfahrens erarbeitet werden konnte. Bei der Frage nach weiteren Bedingungen, die bei der Ausrichtung von Sonnenkollektoren eine Rolle spielen, nannten die Schüler/innen folgende Aspekte:
Bei der sich anschließenden Gruppenarbeit, die bewusst relativ offen formuliert war, war nicht allen Gruppen direkt klar, dass die Schattenbildung bei der Bestimmung des Mindestabstandes eine wichtige Rolle spielt, so dass die Auswertung dieser Phase sich nur auf die Präsentation der Skizze auf einer Folie beschränkte. Die Berechnungen des Abstandes wurden in die Hausaufgabe verlegt.
An den Beiträgen der Schüler/innen und der guten Beteiligung habe ich gemerkt, dass das Thema die meisten Schüler/innen interessiert und sie der Problematik aufgeschlossen gegenüberstehen. Eine Stunde dieser Art lässt sich ideal an unserer Schule ohne großen Aufwand im Zusammenhang mit dem Thema Winkelfunktionen in der Klasse zehn in den Unterricht einbauen.
E. Hölscher
Zurück zur Mathematik-Hauptseite
Zurück zur Fotovoltaik-Hauptseite