| www.r-krell.de |
| Webangebot für Schule und Unterricht, Software, Fotovoltaik und mehr |
Willkommen/Übersicht > Mathematik >
Rezension von Mathematik-Software, Teil e) :
Programme zur Linearen Algebra und Vektorgeometrie
Auf den Seiten a) bis d) berichtete ich über meine Erfahrungen mit bzw. über persönliche Eindrücke von verschiedenen Mathematik-Programmen, nämlich:
a) numerische Programme: Rechen- und Zeichenhilfen
b) interaktive Programme: Lern- und Nachhilfe-Programme:
b1) für die Sekundarstufe I (SI) b2)
für die Sekundarstufe II (SII)
c) Computer-Algebra-Systeme (CAS): Derive, MuPAD und GeoGebra im Vergleich
d) Dynamische Geometrie-Software (DGS): Euklid-DynaGeo, GeoGebra, Z.u.L (Zirkel und
Lineal) im Vergleich
und auf dieser Seite e)
| e) Programme zur Linearen Algebra bzw. Vektoriellen analytischen Geometrie |
zum Seitenanfang / zum Seitenende
Rezension von Mathematik-Software
e) Programme zur Linearen Algebra bzw. Vektoriellen
analytischen Geometrie
Bei der Linearen Algebra und Vektorgeometrie - Stoff in der Jahrgangsstufe 12 - müssen Geraden und Ebenen im R3 in Parameterform oder in anderen Darstellungen notiert werden. Oft soll die gegenseitige Lage von
untersucht werden. Dabei sind die Geraden- und Ebenendarstellungen oft mehrdeutig und i.a. müssen immer wieder lineare Gleichungssysteme gelöst werden. Programme können helfen, fehlerträchtige Routineaufgaben zuverlässig zu lösen und die Lage der Objekte sowohl zu berechnen als auch grafisch zu veranschaulichen. Im besten Falle können die Programme sogar helfen, eine anschauliche Vorstellung vom Geschehen zu vermitteln bzw. sogar zur Entdeckung von Zusammenhängen führen.
Da die vorgestellten Programme zu verschieden sind, wurde hier - anders als in meinen vergleichenden Besprechungen c) und d) - darauf verzichtet, gleiche Aufgaben mit jedem der Programme zu bearbeiten. Vielmehr berichte ich subjektiv, wo und wie ich die Programme verwende und was mir dabei auffiel.
Meine Bildschirmfotos habe ich nachträglich verkleinert bzw. farbreduziert, um ihre Dateigrößen zu verringern und auch Lesern mit langsamem Internetzugang das Betrachten dieser Seite in annehmbarer Zeit zu ermöglichen - die Programme zeigen also größer und schärfer/brillianter an, als hier vermittelt!
Die Tests erfolgten im Januar 2006. Nach der ersten Veröffentlichung der Tests am 9.1.2006 wurden zwei kleinere Fehler, die ich ursprünglich bei Vektor und Analytische Geometrie gerügt hatte, innerhalb weniger Tage beseitigt. Dies spricht für das Interesse der Autoren, Anregungen aufzugreifen und gemeldete Mängel schnellstens zu beheben. Die nachfolgenden Beschreibungen beziehen sich auf die Mitte/Ende Januar 2006 aktuellen, korrigierten Fassungen.
zum Seitenanfang / zum Seitenende
Die CAS-Alleskönner: MuPAD und Derive
Die beiden großen Computeralgebra-Systeme MuPAD und Derive [über die in der Besprechung c) schon berichtet wurde] verfügen über die nötigen Fähigkeiten, um Lineare Algebra zu betreiben. Egal, ob Gleichungssysteme gelöst, Matrizen multipliziert oder invertiert werden sollen oder ob Geraden oder Ebenen definiert und geschnitten werden - immer muss zunächst die entsprechende Struktur in der Syntax des jeweiligen Programms eingegeben werden. Dazu sind Kenntnisse der jeweiligen Befehlssprache des verwendeten Programms nötig und die Handhabung gelingt bei vielen Aufgaben nicht ganz so rasch, wie bei numerisch arbeitenden Spezialisten. Dafür erlauben die CAS-Programme allerdings viel mehr als die nachfolgend besprochenen Programme, können auch mit Parametern arbeiten, führen algebraische Umformungen durch, rechnen exakt mit Brüchen und mit (Form-)Variablen und müssen auch bei mehrdeutigen Lösungen nicht passen. Beide Programme verfügen auch über die Möglichkeit der 3D-Darstellung, wobei MuPAD hier noch flexibler ist.
Angesichts der Fülle der Möglichkeiten würde eine Aufzählung, die den Programmen einigermaßen gerecht werden wollte, den Rahmen dieser Rezension sprengen. Zum Glück gibt es auf den Schulunterricht abzielende Literatur aus berufenem Munde, beispielsweise
sodass ich hier auf weitere Ausführungen verzichten kann. Das auf meiner Webseite „Besprechung von Mathematik-Software: c) Computer-Algebra-Systeme (CAS): Derive, MuPAD und GeoGebra im Vergleich" als Drittes vorgestellte Programm GeoGebra enthält hingegen keine für die Lineare Algebra spezifischen Funktionen und hilft hier nicht.
zum Seitenanfang / zum Seitenende
Numerische Multi-Talente MatheAss und WinFunktion Mathematik
Diese beiden Programme wurden bereits auf meiner Webseite „Besprechung von Mathematik-Software: a) numerische Programme: Rechen- und Zeichenhilfen" vorgestellt, sodass hier ein paar ergänzende Worte reichen sollen.
MatheAss 8 bietet nur wenig für die Lineare Algebra: Gleichungssysteme können gelöst werden (und auch nur, sofern es eine eindeutige Lösung gibt - andere Fälle werden nicht unterschieden), Matrizen können multipliziert und invertiert werden. Weitere Fähigkeiten sucht man vergebens. Ich benutze gelegentlich die Matrix-Funktionen, weil sie schnell zur Hand sind (Für das Lösen von Gleichungssystemen nehme ich natürlich mein eigenes Freeware-Programm LGS_2). Weiter hilft MatheAss nicht.
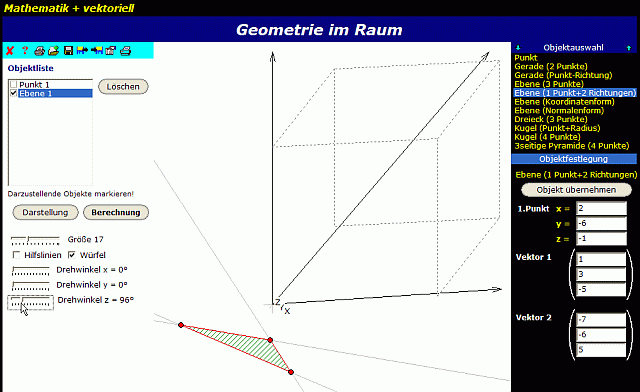
WinFunktion Mathematik bietet in den neueren Versionen sehr viele Möglichkeiten, die nicht immer leicht zu finden sind: In meiner Version WinFunktion Mathematik plus 2002 öffnet sich beim dem Stichwort „vektoriell" das Kapitel „Mathematik + vektoriell", wo Punkte, Geraden und Ebenen eingegeben werden können und in eine Objektliste übernommen werden. Mit der Schaltfläche „Darstellung" werden die in der Objektliste mit Häkchen versehenen Objekte angezeigt: Ebenen werden durch ein Dreieck repräsentiert; einzelne Punkte sind offenbar nicht zu sehen.


Die Bedienung ähnelt z.T. der von Geo 1.13
(s.u.), bei dem mir allerdings die Umwandlungen etwas besser gefallen und wo das Vorgehen besser vom Benutzer
kontrolliert werden kann. Insofern - und weil WinFunktion
Mathematik leider immer den ganzen 1024x768er-Bildschirm beansprucht und sogar die Taskleiste
verdeckt und damit der Wechsel zu anderen geöffneten Anwendungen nur mit dem mühsamen Umweg über den
Task-Manager möglich ist - benutze ich WinFunktion
Mathematik trotz seiner zweifellos vorhandenen Möglichkeiten nur selten für die
Lineare Algebra, kenne mich also auch nicht besonders gut damit aus. Dabei löst (unter dem Stichwort
„algebraisch") dieses Programm auch mehrdeutige lineare Gleichungssysteme richtig und gibt die Lösungen
mit Parametern an (wobei leider zusätzlich der irreführende Hinweis 'unlösbar' erscheint;
Zwischenschritte des Gauß-Algorithmus werden angezeigt!) und beherrscht auch die Matrizenrechnung (und kann
z.B. bei der Matrixmultiplikation auch mit Zwischenergebnissen weiter rechnen -- während bei MatheAss ärgerlicherweise erhaltene Ergebnismatrizen von
Hand nochmal eingetippt werden müssen, wenn man damit weiter rechnen will). Wer WinFunktion Mathematik gekauft und installiert hat, kann damit
also durchaus zum Thema arbeiten. Zumal die eingegebenen und in die Liste aufgenommenen Objekte durch Klick auf das
Diskettensymbol speicherbar sind und schon gespeicherte Objektlisten auch später wieder geöffnet werden
können, sodass beispielsweise alle in einer Klausur vorkommenden Geraden und Ebenen gemeinsam gesichert und zur
Korrektur wieder geholt werden können (Über eine solche wünschenswerte Objektverwaltung verfügen
von den nachfolgend besprochenen Programmen leider nur noch Geo und AG-Analytische Geometrie).
Die anschauliche Hilfe von WinFunktion Mathematik
hält einige durchgerechnete Beispielaufgaben bereit und kann so auch als (allerdings recht knappe) Anleitung
für Schülerinnen und Schüler dienen. Die Tests und abgebildeten Bildschirmabdrucke wurden wie
angegeben mit meiner plus-Version von 2002 durchgeführt, die auch als Version XII bekannt ist. Anfang 2006 wurde
die aktuelle Version 15, also WinFunktion Mathematik plus
V.15, beim bhv-Verlag
für knapp 27 bis 30 € angeboten; ältere Versionen findet man z.T. auch noch - preisreduziert - im
Handel.
zum Seitenanfang / zum Seitenende
Numerisches Multi-Talent MathProf
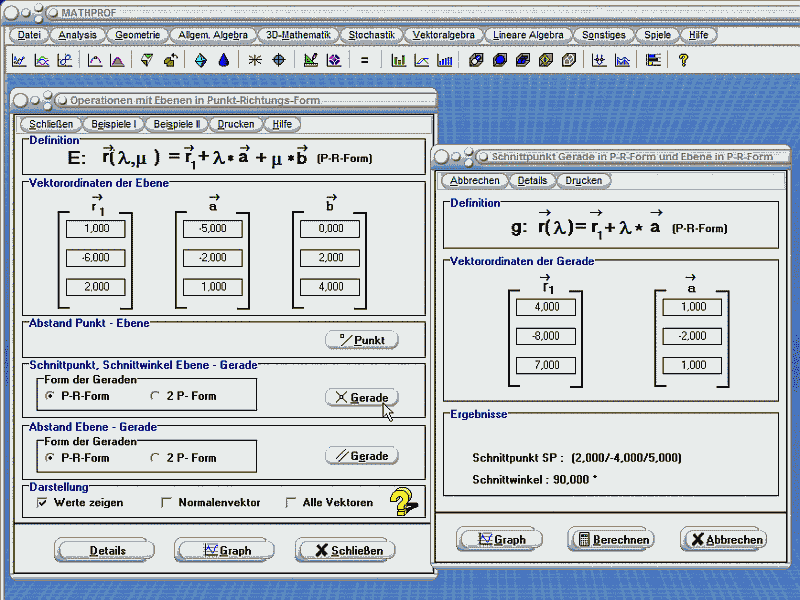
Zusammen mit den beiden vorgenannten Programmen wurde auf meiner Seite „Besprechung von Mathematik-Software: a) numerische Programme: Rechen- und Zeichenhilfen" auch MathProf 2.0 vorgestellt, das mir bisher durchaus reichte. Für diesen Test habe ich mir aber extra auch die aktuelle Version MathProf 4.0 angesehen, für die inzwischen die Fa. ReduSoft verantwortlich zeichnet. Augenfällig sind die neue Oberfläche und einige Erweiterungen, allerdings weniger im hier untersuchten Bereich: In den Menüs „Geometrie" (u.a. Affine Abb., Pyramide, Kugel, Kegel, Torus, Zylinder und Quader), „Lineare Algebra" (Matrizen, Determinanten, LGS) und vor allem „Vektoralgebra" findet man viele hier interessante Funktionen. U.a. kann man (wie sonst nur noch in WinFunktion Mathematik) die einzelnen Umformungsschritte des Gauß-Algorithmus beim Lösen eines Linearen Gleichungssystems einzeln verfolgen. Das Programm ist leicht und intuitiv bedienbar; allerdings lassen sich die eingegeben Objekte nicht abspeichern und verschwinden beim Schließen des jeweiligen Fensters. Will man den Schnitt einer Gerade und einer Ebene ermitteln, muss zunächst aus dem Menü „Vektoralgebra" der Menüpunkt „Ebene - Gerade/Punkt (3D)" gewählt und dann eine von vier Darstellungsformen der Ebenengleichung gewählt werden. Nach Eingabe der Ebene können im entsprechende Dialog mit „Details" andere Darstellungsformen der Ebene (neben der Parameterform auch drei die Ebene bestimmende Punkte, die Normalen- und die Koordinatenform) angesehen werden. Auch die Spurpunkte werden hier angegeben. Mit der Schaltfläche „Gerade" im Ebenen-Dialog kann ein weiteres Fenster zur Eingabe eine Gerade geöffnet werden (eine eventuell früher unter dem eigenen Menüpunkt Gerade eingegebene Gerade erscheint nicht wieder und muss hier neu eingegeben werden). Dann wird nach „Berechnen" der vorhandene Schnittpunkt angezeigt (s. oberes Bild). Schade: wird der Abstand eines Punktes von der Ebene bestimmt, wird dieser zwar ermittelt, leider aber nicht der Fußpunkt des Lots angegeben.
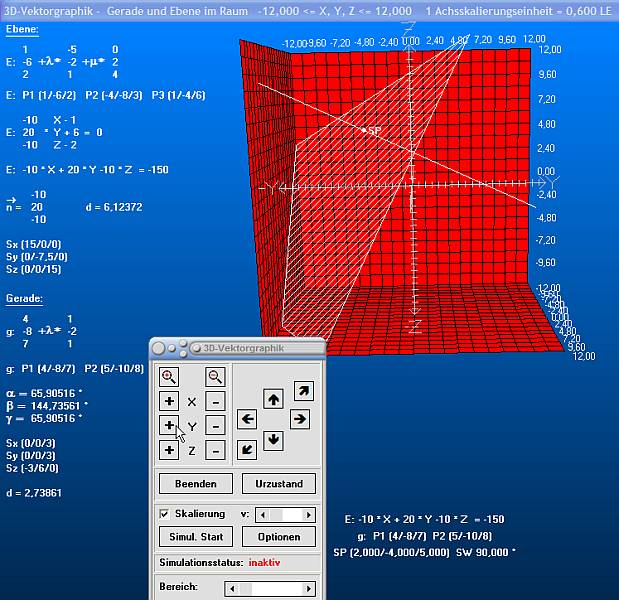
Sehr anschaulich ist die Grafik von MathProf: in einem skalier-, vergrößer-/verkleiner-, verschieb- und drehbaren Koordinatensystem werden Geraden und Ebenen so angezeigt, dass man zumindest nach einigen Drehungen ein gute Vorstellung von ihrer Lage im Raum erhält! Auf einem Vollbild-Grafikfenster erscheint die folgende anschauliche Darstellung, wenn oben „Graph" gedrückt wird:
Für die Software-Funktionen gibt es oft mehrere Beispiele und eine ausführliche Hilfe, die die Bedienung des Programms erläutert und i.a. auch die Lösung eines Beispiels enthält (aber nicht das mathematische Verfahren erklärt wie Vektor, s.u.). Anfang 2006 wurde die Version 4.0 für rund 30 €uro bei www.mathprof.de angeboten. Dort steht auch eine kostenlose Demo zum Download bereit.
zum Seitenanfang / zum Seitenende
Spezialprogramm Geo 1.13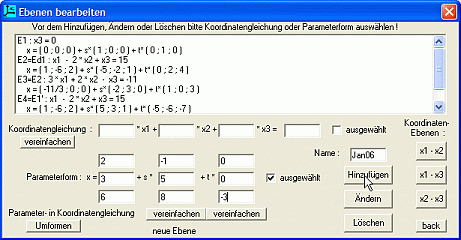
Als kostenloses Tool erfreut Geo (auch
„Geo.exe" genannt) von Rainer Müller.
Das Programm ist Freeware und kann von www.emath.de herunter
geladen werden. Die Version 1.13 (vom Mai 2005) war auch Anfang 2006 noch aktuell (Downloadgröße ca. 2,3
MB).
Zur schnellen Kontrolle von Aufgabenlösungen, aber auch zum Weiterrechnen mit falsch bestimmten Geraden und
Ebenen während der Klausurkorrektur gehört Geo zu den Programmen, die ich immer wieder nutze. Die Objekte
- möglich sind Punkte, Vektoren, Geraden, Ebenen und Kugeln - können meist auf verschieden Arten in
spezielle Masken leicht eingegeben, verändert und dem Bestand hinzugefügt (oder daraus auch wieder
gelöscht) werden. Ärgerlich ist allerdings, dass alte Eingaben beim Anklicken oder Betreten eines
Eingabefelds nicht automatisch blau markiert werden, sodass beim Eingeben eines zweiten, gleichartigen Objekts immer
erst die alten Werte zeichenweise gelöscht werden müssen. Die gegenseitige Lage von Objekten im Bestand
kann unter dem Menüpunkt „Lage/Schnitt" gezielt ermittelt werden (nach Wahl eines Menüpunktes, z.B.
„Gerade - Ebene" werden alle Geraden und alle Ebenen im Objektbestand in zwei Listen genannt und die beiden zu
untersuchenden lassen sich per Mausklick wählen), wobei dann auch automatisch Abstände, Lotfußpunkte
oder Schnittgeraden ausgegeben werden.
Zu Recht werden auf der eMath-Webseite u.a. folgende Fähigkeiten von Geo genannt:
Allerdings eignet sich Geo vor allem zum (Be-)Rechnen. Die Zeichnungen im skalier-, aber nicht drehbaren Koordinatensystem sind wenig anschaulich, müssen etwas mühsam über das Menü „Bild" angefordert werden und können nicht überzeugen. (Anklicken der hier verkleinerten Bilder öffnet diese größer bzw. vergrößerbar in einem neue Browser-Fenster - in Geo selbst lassen sich die Fenstergrößen übrigens nicht ändern! Außerdem liefert die knappe Hilfe nur Hinweise zur Bedienung des Programms, nicht zur Mathematik):
zum Seitenanfang / zum Seitenende
Spezialprogramm Vektor 1.9 (GeoSekII)
Unter dem Namen Vektor bietet Roland Bernert die (32-Bit-)Neuauflage seiner früher unter dem Namen GeoSekII bekannten (und ebenfalls noch erhältlichen 16-Bit-) Software zur Linearen Algebra und Vektorgeometrie an. Das Programm ist kostenlos und kann von der Homepage http://www.lehrer.uni-karlsruhe.de/~za186/ herunter geladen werden. Anfang 2006 war dort Vektor in der Version 1.9 vom Januar 2006 erhältlich (Downloadgröße nur ca. 500 kB; Inhalt des zip-Archivs einfach in ein neuen Ordner entpacken und vektor.exe z.B. durch Doppelklick starten).
Der Funktionsumfang von Vektor geht noch über den des vorstehend beschriebenen Programms Geo hinaus: Bei Vektor sind z.B. auch Matrizenmultiplikationen (aber nur 2x2 bzw. 3x3) und Spatprodukt sowie affine Abbildungen, Dreiecke und Ellipsen im R2 möglich. Lineare Gleichungssystem können nur in den Größen 2x2 oder 3x3 und nur bei eindeutiger Lösung gelöst werden.
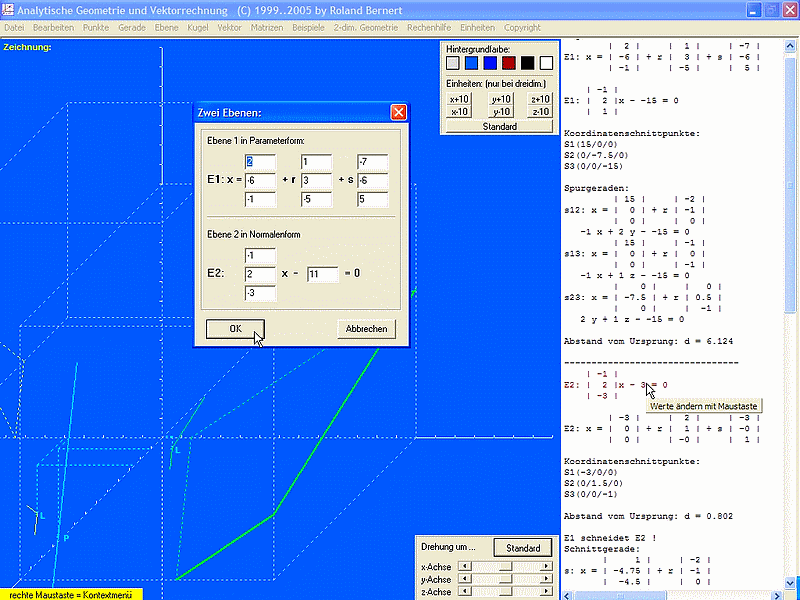
Bei der (automatischen) graphischen Darstellung ist das Koordinatensystem verschieb- und drehbar; weitere Hilfslinien wie etwa die Spurgeraden von Ebenen lassen sich mit rechtem Mausklick (und entsprechende Wahl im Kontextmenü) zusätzlich einblenden. So kann ein etwas besserer Eindruck der räumlichen Lage von Objekten vermittelt werden. Hervorzuheben ist, dass alle Objekte nachträglich per Mausklick verändert werden können, um z.B. für eine „schöne" Schnittgerade oder eine bestimmte Lage im Raum zu sorgen: Nach Klick auf jede ursprünglich eingegebene Zahl im rechten, weißen Ergebnisfenster kann diese mit linkem oder rechtem Mausklick in Einerschritten erhöht bzw. erniedrigt werden: Die graphische Darstellung und alle Ergebnisse passen sich sofort automatisch an! (Das ursprüngliche Eingabefenster, unten im Bild zur Information nochmal einmontiert, verschwindet dabei). Diese Fähigkeit erleichtert Lehrerinnen und Lehrern die Konstruktion von Aufgaben und ermöglicht Schülerinnen und Schülern, den Einfluss jeder Zahl in einer Gleichung auf das Objekt bzw. seine Lage zu studieren.
Erscheint Vektor (mit Ausnahme des Gleichungssystemlösers, aber dafür gibt's ja mein LGS_2) damit besser und vielseitiger als Geo (und fällt auch die Eingabe leichter, weil alte Werte in Eingabefeldern vollständig markiert werden und daher leichter zu ändern sind), so stört hingegen wie bei MathProf das Fehlen einer Objektverwaltung. Wurden z.B. schon zwei Ebenen in Parameterform eingegeben und soll dann deren Schnitt berechnet werden, müssen die Gleichungen erneut eingetippt werden (während eine Ebene in Parameter- und eine in Normalenform auch später noch ohne Neueingabe verglichen werden können). Stehen also mehrere Objekte in unterschiedlicher Beziehung, ist die Rechnung mit Geo leichter, weil dort der Bestand gespeichert wird und damit später erneut auf schon eingegebene Objekte zugegriffen werden kann. So etwas fehlt bei Vektor leider.
Andererseits sind für viele Funktionen von Vektor Beispiele verfügbar und eine anklickbare (und ausdruckbare) mathematische Rechenhilfe erläutert ausführlich und gut das jeweilige Vorgehen und vermittelt Schülerinnen und Schülern so das Rezept zum Lösen ähnlicher Aufgaben (die Hilfe-Texte sind auch als .rtf-Dateien im Programmverzeichnis zu finden und können mit Textverarbeitern geöffnet und verwendet werden). Im Übrigen arbeitet Vektor immer mit einem 1024x768er-Bildschirm. Wird von Windows die Taskleiste nicht automatisch versteckt, verdeckt diese unten einen Teil des Vollbild-Fensters (unter Windows sollte dann mit Start > Einstellungen > Taskleiste und Startmenü das automatische Ausblenden gewählt werden). Zeichnungen können außer im .bmp-Format sinnvollerweise auch in den Vektorformaten .wmf und .emf gespeichert werden - nach Wahl schwarz/weiß oder farbig; der rechts angezeigte Streifen mit Ergebnissen kann ebenfalls als Bild gespeichert werden (aber eben nur als Bild in den genannten Formaten, nicht etwa auch als Textdatei zur weiteren Verarbeitung). Objekte selbst können nicht gespeichert werden; auch können keine früheren Informationen oder Daten von Vektor geöffnet bzw. wieder eingelesen werden.
zum Seitenanfang / zum Seitenende
Spezialprogramm AG 2.0 - Analytische Geometrie
Der Autor Werner Pieper hat dieses aus seiner mathe-quelle.de als Shareware erhältliche Programm geschrieben, um Schülerinnen und Schülern - z.B. während des Mathematik-Unterrichts im Computerraum - die mathematische Beschreibung etwa einer Gerade oder Ebene direkt bildlich zu veranschaulichen (indem beispielsweise der Einfluss einer bestimmten Koordinate des Richtungsvektors auf die Lage der Gerade untersucht wird). Oder die Lernenden werden aufgefordert, eine Kugel zu finden, die einen vorgegebenen Punkt berührt, um dann dort die Tangentialebene zu konstruieren. Mit verschiedenen, z.T. auch in der Hilfe aufgeführten Aufgaben und dort beschriebenen Aufgabentypen sollen die Schülerinnen und Schüler jedenfalls das Konstruieren im R3 lernen und praktizieren, Konstruktionsbeschreibungen abfassen und/oder nachvollziehen und eine anschauliche Vorstellung der Zusammenhänge in der Vektorgeometrie gewinnen.
Darüber hinaus kann das Programm natürlich wie die oben vorgestellte Software auch zum raschen Lösen und Zeichnen vieler Schnittprobleme verwendet werden. Auch die Berechnung und Darstellung von Spaten, Kugeln und Kegeln sowie die Matrizenrechnung (Produkt und Determinante) sowie das Vektorprodukt sind verfügbar.
Als Objekte können gleichzeitig 3 Geraden, 2 Ebenen und jeweils 4 Spate, 4 Vektoren, 4 Strecken, 4 Punkte, 4 Kugeln und 4 Kegel verwaltet, gemeinsam gespeichert und in eine späteren Sitzung wieder komplett eingelesen und weiter verwendet werden. Normalerweise sollte dies längst reichen; nur gelegentlich wird der Wunsch auch nach 4 Geraden oder 4 Ebenen laut.
Mit der nur auf den ersten Blick etwas überladen wirkenden Werkzeugliste am oberen Bildschirmrand können die Objekte durch bequemes Anklicken einzeln sichtbar/unsichtbar geschaltet, gefärbt und/oder zur Drehung freigegeben werden. Die Eigenschaften werden in eigenen Dialogen (über das Menü erreichbar) festgelegt, wobei z.B. für die Eingabe einer Ebene neben der Parameterform auch die Koordinaten- oder die Normalenform möglich ist, und Analytische Geometrie 2.0 automatisch in die übrigen Formen umwandelt. Im skalier-, vergrößer-/verkleiner-, verschieb- und drehbaren Koordinatensystem lassen sich die Ebenen (wie aus nachfolgendem Bild ersichtlich) auf verschiedene Weise zeichnen, sodass auch sehr anschauliche Darstellungen gelingen. Zusätzlich beherrscht Analytische Geometrie 2.0 noch verschiedene einstellbare Projektionen bzw. Perspektiven (u.a. Aufriss, Kreuzriss, Grundriss), erlaubt die Eingabe von Drehmatrizen, und mehr.
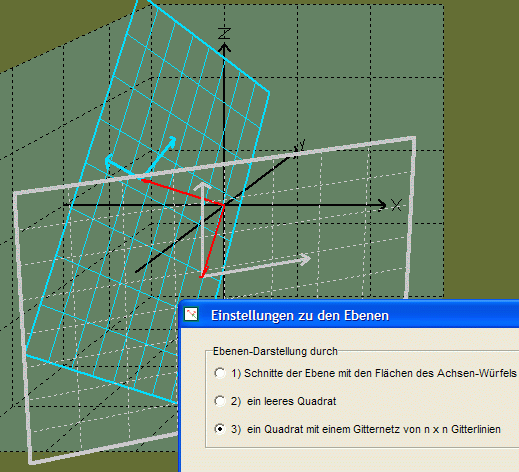
Ebenfalls über die anderen hier besprochenen numerischen Programme deutlich hinaus geht außerdem die Fähigkeit von Analytische Geometrie 2.0, Objekte in der Graphik auch einzeln oder in Gruppen zu drehen (um die Koordinatenachsen oder beliebige eigene Geraden), während das Programm gleichzeitig ihre Gleichungen neu anpasst. Damit sind (wie z.T. bei Vektor, hier aber noch vielseitiger und nicht auf jeweils eine Zahl der Gleichung beschränkt) nachträgliche und leichte Änderungen an den Objekten möglich, bis ihre Wunschlage erreicht ist. Aber auch das Ändern einzelner Zahlen in einer Ebenen- oder Geradengleichung (z.B. rasch hintereinander in Zehntel-Schritten bequem durch Festhalten eines Mausschalters, während die Änderungen filmartig angezeigt werden) ermöglicht Analytische Geometrie 2.0 - diese Fähigkeit findet man bei „Animation". Beides hilft, wie oben gesagt, dem Lehrer bei der Konstruktion von Aufgaben und/oder kann Schülerinnen und Schülern den Zusammenhang zwischen der geometrischen Lage eines Objekts und seiner formelmäßigen Beschreibung erfahrbar und deutlich machen, zumal Analytische Geometrie 2.0 wichtige Bestimmungsstücke (etwa der Stütz- und die Richtungsvektoren einer Ebene) nicht nur verändert, sondern auch mit anzeigt.
Unter dem Menüpunkt „Ergebnisse" lassen sich zudem (wie bei den besseren der anderen Programme) die Schnitte gezielt ausgewählter Objekte rechnerisch bestimmen und anzeigen. Der Autor berichtet, dass er bei der Auswahl der angezeigten oder zu übernehmenden Ergebnisse einen Kompromiss zwischen Vollständigkeit und Verbergen einiger Werte gesucht hat (um Schülerinnen und Schüler noch zu eigenen Rechnungen zu zwingen). Außerdem können wohl bei einigen Aufgaben Koordinaten vor Schülern versteckt werden.
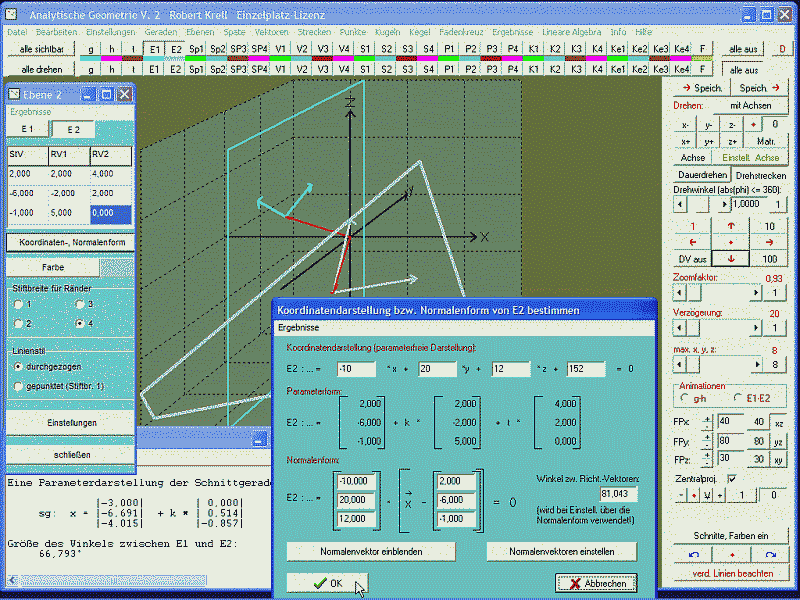
Die Grafiken lassen sich im .bmp-Format wie auch im (für spätere Vergrößerungen oder Verkleinerungen besseren) .wmf-Vektorformat speichern, die Objekte können - wie bereits lobend erwähnt - gespeichert und später wieder geöffnet werden und sogar Grafik- bzw. Perspektiveinstellungen, Farbwahlen u.ä. lassen sich festhalten. Es dauert einige Zeit, bis man alle Fähigkeiten des Programms entdeckt. Drei in der Hilfe enthaltene „Einführungen" helfen zumindest bei den ersten bzw. wichtigsten Schritten. Die Hilfe enthält neben der Bedienungsanleitung auch zwei Beispielaufgaben für die Selbsttätigkeit von Schülern sowie Tipps für Lehrer (aber keine allgemeinen mathematischen Lösungsweg-Beschreibungen wie bei Vektor). Auf der Mathe-Quelle-Homepage gibt's weitere Hinweise und Beispiele. Download ca. 750 kB; nach einer kostenlosen Prüfphase beträgt die Registriergebühr für Analytische Geometrie 2.0 rund 30 € für die Einzellizenz; 70 € für die Schullizenz und 120 € für die erweiterte Schullizenz inkl. aller Schüler.
zum Seitenanfang / zum Seitenende
zurück zur „Mathematik"-Hauptseite